<twoyao>
我们知道,NP-Complete问题总是可以在多项式时间内验证一个答案,但无法在多项式内求解的问题,对于这类问题往往使用brute-force搜索,虽然用递归写来简单,但并不高效。Knuth在2000曾提出Algorithm X 算法用于解决Exact cover 问题, 算法优雅简单,但知道的人不多,值得本文在此安利一下。
双向链表的一个特性
假如x为双向链表中的一个元素,right和left指向其前后元素,那么
x.right.left = x.left, x.left.right = x.right将会把x元素从链表中移除。但更奇特的是下面这步操作
x.right.left = x, x.right.left = x可以将x元素放回链表,而这些操作仅仅涉及x一个变量。Knuth将其称之为Dancing Links。
有洁癖的程序员可能会在移除x后将right和left设置为null或者x自身,大部分情况下这是正确的做法,但是如果不回收x,这种特性在回溯(深度优先搜索)中非常有用。我们先从Exact cover问题出发描述如何使用该方法,你将会看到Algorithm X惊人高效回溯速度及简单的启发。
Exact cover problem(精确覆盖问题)
给定一个均是0和1的矩形,是否存在这样一个行的集合,它精确覆盖了每列的1。例如下面的1、5及3、4就是这样一个集合;1、3则不行,因为第二列的1有两个,不满足精确覆盖。
0 1 1 0 // 1
0 0 0 1 // 2
1 1 0 1 // 3
0 0 1 0 // 4
1 0 0 1 // 5假设有一个01矩阵A,Algorithm X 通过穷举求解,伪代码描述如下
1. If A is empty, the problem is solved; terminate successfully.
2. Otherwise choose a column, c (deterministically).
3. Choose a row, r, such that A[r, c] = 1 (nondeterministically).
4. Include r in the partial solution.
5. For each j such that A[r, j] = 1,
delete column j from matrix A;
for each i such that A[i, j] = 1,
delete row i from matrix A.
6. Repeat this algorithm recursively on the reduced matrix A用Dancing Links如何实现Algorithm X呢?比方说,A矩阵长这样
// A B C D E F G
0 0 1 0 1 1 0 // 1
1 0 0 1 0 0 1 // 2
0 1 1 0 0 1 0 // 3
1 0 0 1 0 0 0 // 4
0 1 0 0 0 0 1 // 5
0 0 0 1 1 0 1 // 6我们用Node表示其中1 的节点, Column表示列,len表示这列中1的个数,name表示这列的名称(用于输出结果),比如Column-B.len = 2, Column-B.name = "B"
class Node {
Node left, right, up, down;
Column col;
}
class Column extends Node{
String name;
int len;
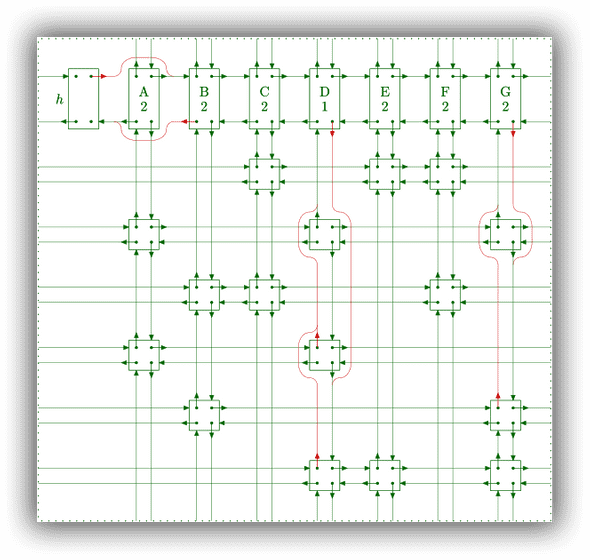
}矩阵A用上述结构描述的结果如下图所示,head(h) 是为了方便代码处理的列头,本身并不属于具体任何一列或行。
使用上面的数据结构,有任一答案后马上返回的递归实现如下,k表示搜索深度,最初调用search(0)
public boolean search(int k) {
if (head.right == head) {
return true;
}
Column bestCol = bestColumn();
if (bestCol.len == 0) {
return false;
}
cover(bestCol);
for (Node r = bestCol.down; r != bestCol; r = r.down) {
choices.add(r);
for (Node j = r.right; j != r; j = j.right) {
cover(j.col);
}
boolean ret = search(k + 1);
if (ret) return true;
choices.remove(choices.size() - 1);
for (Node j = r.left; j != r; j = j.left) {
uncover(j.col);
}
}
uncover(bestCol);
return false;
}每次调用需要选择一列(bestCol),最简单的实现可以是bestCol = head.right 。Knuth在论文中实验证明:选择长度最小的那列(分支少)可以有效地提高搜索效率。
private Column bestColumn() {
int minLen = Integer.MAX_VALUE;
Column bestCol = null;
for (Column curr = head.right; curr != head; curr = curr.right) {
if (curr.len < minLen) {
bestCol = curr;
minLen = curr.len;
}
}
return bestCol;
}cover 将列col从head list 中移除,并将col涉及到的所有行移除
private void cover(Column col) {
col.left.right = col.right;
col.right.left = col.left;
for (Node i = col.down; i != col; i = i.down) {
for (Node j = i.right; j != i; j = j.right) {
j.up.down = j.down;
j.down.up = j.up;
--j.col.len;
}
}
}与 cover对立的操作uncover将恢复cover造成的影响,也是前面双向链表性质的应用
private void uncover(Column col) {
for (Node i = col.up; i != col; i = i.up) {
for (Node j = i.left; j != i; j = j.left) {
j.up.down = j;
j.down.up = j;
++j.col.len;
}
}
col.right.left = col;
col.left.right = col;
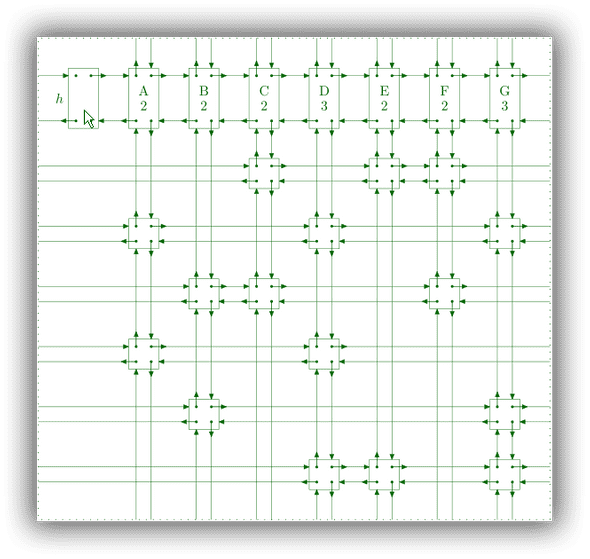
}uncover 的操作和cover的操作循环的属性正好相反,遵守这点非常重要。第一次调用,search(0) 时,最短的列是长度为2的A,cover A列后结构变成下面这样
最后,矩阵A精确覆盖的唯一解(row sets)是{1, 4, 5}。代码工程将在文末给出。
求解其他NP-Complete问题的方法就是将其转化成Exact Cover 后求解,数独就是这样一类问题。
Soduku(数独)
数独问题就是将数字1-9填入9x9的格子并满足横竖宫都具有1-9,只求一个解法的数独问题正是NP-C问题,求所有解法的则是NP-hard问题,所以数独可以约化成精确覆盖问题求解。
在9x9数独中,9x9格子每个格子填入9个数字,这就有9x9x9=729种填法,用R表示行,C表示列,#表示数字,每种填法可以表示成
R1C1#1, R1C1#2, …, R9C9#9.
每种填法均需满足4种约束,所有填法的约束集不能有交集:
- **Row-Column: ** 每个格子仅能填一个数字。例如列1行1只能填一个数字,将该约束集记为R1C1,则包含9个数字的所有可能填法 R1C1 = { R1C1#1, R1C1#2, R1C1#3, R1C1#4, R1C1#5, R1C1#6, R1C1#7, R1C1#8, R1C1#9 }.
- Row-Number: 每行必须包含1-9各一次。例如行1只能包含一个1,将该约束集记为R1#1,则包含9列的所有可能填法 R1#1 = { R1C1#1, R1C2#1, R1C3#1, R1C4#1, R1C5#1, R1C6#1, R1C7#1, R1C8#1, R1C9#1 }.
- Column-Number: 每列必须包含1-9各一次。例如列1只能包含一个1,将该约束集记为C1#1,则包含9行的所有可能填法 C1#1 = { R1C1#1, R2C1#1, R3C1#1, R4C1#1, R5C1#1, R6C1#1, R7C1#1, R8C1#1, R9C1#1 }.
- Box-Number: 每宫必须包含1-9各一次。例如宫1只能包含一个1,将该约束集记为B1#1,则所有可能填法 B1#1 = { R1C1#1, R1C2#1, R1C3#1, R2C1#1, R2C2#1, R2C3#1, R3C1#1, R3C2#1, R3C3#1 }.
欲将数独问题转化为精确覆盖问题,9行9列9数表示该矩阵有9x9x9=729 行;四种约束,每种81个,所以该矩阵有81 x 4 = 324 列。所有的矩阵分布情况请看The complete 729×324 matrix is available from Bob Hanson
举例来说R2C4#1对应的行应该是怎样的呢?4个约束表示该行324列中应有4个1。用前81列表示第一个约束Row-Column ,R2C4可以标在9x(2-1)+4-1=12,减一是因为列索引从0开始;用第二个81列表示第二个约束Row-Number,R2#1可以标在9x(2-1)+1-1+81=18=90位;用第三个81列表示第三个约束Column-Number ,C4#1可以标在9x(4-1)+1-1+81x2=189;用第四个81列表示第四个约束Box-Number B2#1可以标在9x(2-1)+1-1+81*3=252,R2C4属于第二宫(正上)。所以R2C4#1对应的列为
0 0 0 0...1(12)...1(90)...1(189)...1(252)我曾使用DLX过POJ-3074-Sudoku ,速度在前十之列,完整的代码在这 。需要说明的是,DLX求解数独并不是最快的,最高效地是利用数独规则减少搜索分支。
最后,如果你坚持看到了最后,估计也想吐槽才两个问题也好意思说”应用”? 改日补上~ 所有工程代码在这。
References
- Knuth, Donald (2000). “Dancing links”. arXiv:cs/0011047.
- Exact_cover
- solving-sudoku-with-dancing-links
- Knuth’s Algorithm X
- NP-completeness